deliveryrest.blogg.se

With F as centre and taking same radius, draw another arc that cut the previous arc at H. (x) With Z as centre and taking radius more than half of ZF, draw an arc. (ix) With Y as centre and taking convenient radius, draw two arcs that intersect ZX at Z and F.

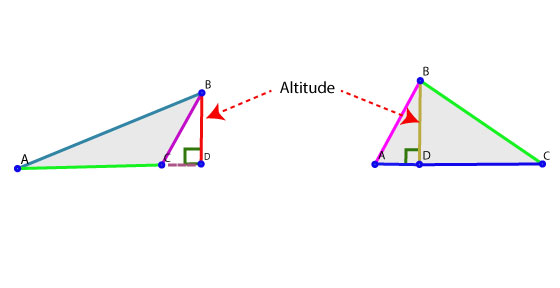
(vii) Draw the perpendicular bisector IJ of the side ZX that intersect ZX at K. With B as centre and taking same radius, draw another arc that cut the previous arc at C. (v) With A as centre and taking radius more than half of AB, draw an arc. (iv) With X as centre and taking convenient radius, draw two arcs that intersect YZ at A and B. (ii) Draw the perpendicular bisector DE of the side YZ that intersect YZ at L. Hence, ∆LMN is the required triangle in which the altitudes LI, MK and NJ to the sides MN, NL and ML respectively intersect at O. NJ is an altittude to the side ML produced. (xii) Join NC that intersect ML produced at J. With B as centre and taking same radius, draw another arc that intersect the previous arc at C. (xi) With A as centre and taking radius more than half of AB, draw an arc. (x) With N as centre and taking convenient radius, draw two arcs that intersect ML produced at A and B. (viii) Join MF that intersect NL produced at K. With E as centre and taking same radius, draw another arc that intersect the previous arc at F. (vii) With D as centre and taking radius more than half of DE, draw an arc. (vi) With M as centre and taking convenient radius, draw two arcs that intersect NL produced at D and E. With Q as centre and taking same radius, draw another arc that intersect the previous arc at R. (iii) With P as centre and taking radius more than half of PQ, draw an arc. (ii) With L as centre and taking convenient radius, draw two arcs that intersect MN at P and Q.